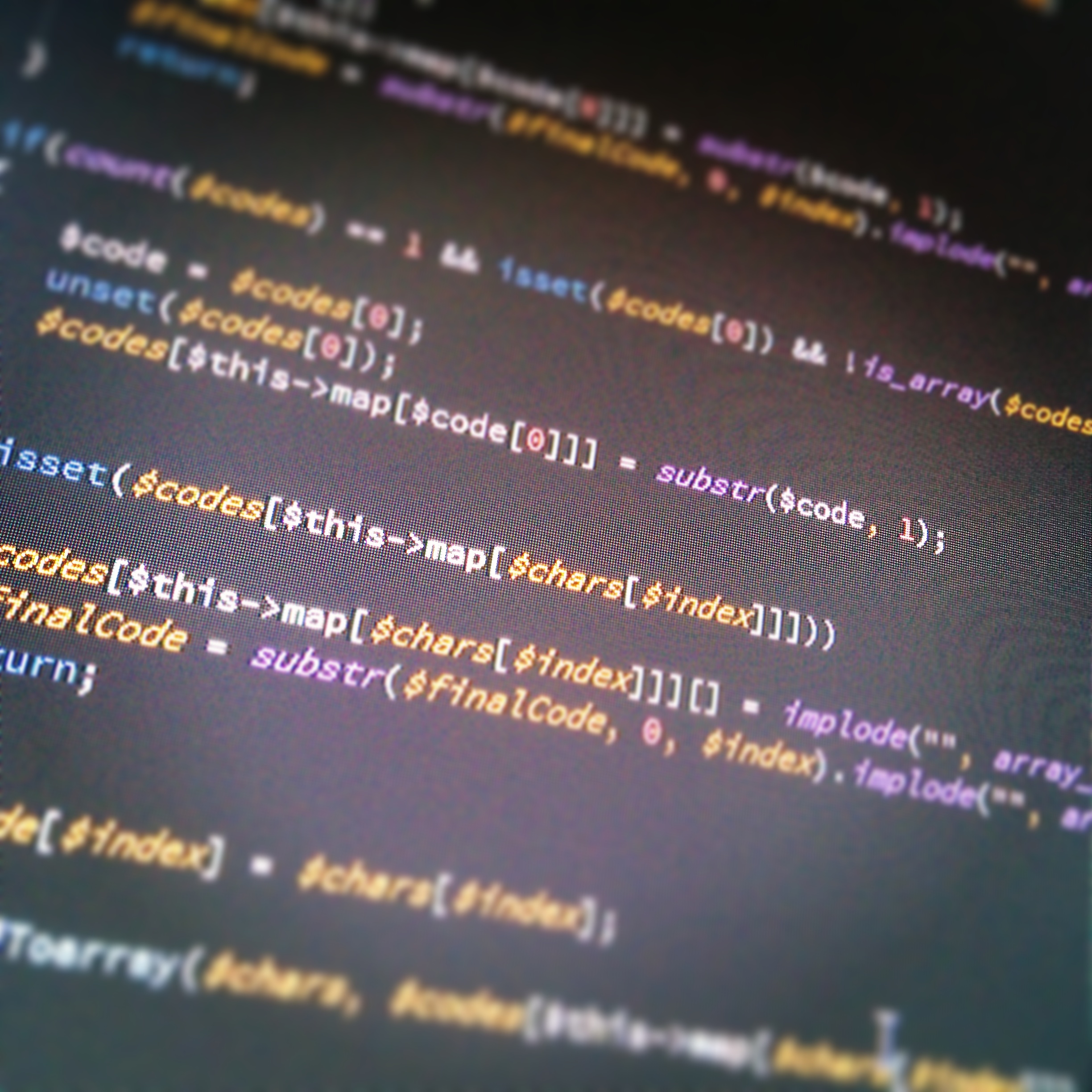
Generating pseudo random codes is usually a trivial task. However, coupon codes should have two features that make them computationally complex:
- They have to be unique
- They should be hard to guess
A third optional feature would be readability. This means that the final user should not be thinking “is this 0 or O?“.
I found the problem intriguing and decided to make my personal implementation of a coupon code generator in PHP.
First of all, I defined a class with some properties:
$fromCharsand$toCharsare used to solve the readability problem. Chars in the$fromCharsstring are mapped 1:1 with chars in the$toCharsstring. I got this solution from here.$mapis used to translate chars in numerical indexes. You’ll see later why this is useful.$lengthis the number of chars in the generated code.
If you stumble upon memory issues with PHP, just uncomment the first line and adjust it to your requirements.
//ini_set('memory_limit','255M');
class RandomCodeGenerator {
private $fromChars = "0123456789abcdefghij";
private $toChars = "234679QWERTYUPADFGHX";
private $length = 10;
private $useLetters = true;
private $map = [
"2" => 0,
"3" => 1,
"4" => 2,
"6" => 3,
"7" => 4,
"9" => 5,
"Q" => 6,
"W" => 7,
"E" => 8,
"R" => 9,
"T" => 10,
"Y" => 11,
"U" => 12,
"P" => 13,
"A" => 14,
"D" => 15,
"F" => 16,
"G" => 17,
"H" => 18,
"X" => 19
];
/**
* @return int
*/
public function getLength()
{
return $this->length;
}
/**
* @param int $length
*/
public function setLength($length)
{
$this->length = $length;
}
/**
* @return boolean
*/
public function isUsingLetters()
{
return $this->useLetters;
}
/**
* @param boolean $useLetters
*/
public function useLetters($useLetters)
{
$this->useLetters = $useLetters;
}
}And now we’re ready for the main function. To generate hard to guess codes I used the function openssl_random_pseudo_bytes. It produces a numer of random bytes equal to the length parameter. For this number, I used the specified code length, although the required minimum length is somewhere around (code_length / 2) + 1, but it depends on the base value (see below).
To be more specific, you could implement a dinamically determined value for the amount of bytes to generate. You could start with a certain amount (i.e. 0 or half the code length), and then increment it if necessary. At every iteration, you should check wether the code you generated is sufficiently long. If not, add 1 to the minimum number of bytes and re-generate the code.
To obtain a sequence of chars, the array of bytes is converted to hex. Then, switching to base 20 you get a string using up to 20 different chars (“0123456789abcdefghij“). Of course, if you need more or less chars you can adjust the base accordingly. For instance, base 10 is used to generate numeric codes.
My first attempt was a really simple function that checked uniqueness with PHP’s in_array function. You’ll find the code below. Needless to say, this function was utterly inefficient.
function generate($amount)
{
$codes = [];
do
{
$number = bin2hex(openssl_random_pseudo_bytes($this->length));
if($this->useLetters)
{
$string = base_convert($number, 16, 20);
$string = strtr($string, $this->fromChars, $this->toChars);
}
else{
$string = base_convert($number, 16, 10);
}
$string = substr($string, 0, $this->length);
if(!in_array($string, $codes))
$codes[] = $string;
} while(count($codes) < $amount);
return $codes;
}Despite being light on memory usage, the time required by this function grows exponentially (see the charts below).
A quick look at the code and you’ll see there are many ways it could be improved. However, the huge bottleneck that needed extreme optimizations was clearly the in_array function.
My first approach at fixing this bottleneck was to create a tree from the generated codes (using associative arrays). The first layer of siblings (or separate root nodes, as you like) represented the first letter of the codes. Following a path from one of the root nodes to one of its leaves would represent an existing code. An example can be seen in the second column of the image below (the one called “fully indexed approach”).
Although this algorithm’s time to complete grew linearly, it introduced a memory usage problem. Having to create a complete path down the tree for each code made memory usage grow exponentially, just like the original algorithm did with time.
That being said, let’s talk about the “final” (for now) algorithm.
Let’s start with a list of simple optimizations:
- The final list of generated codes is a
SplFixedArray. This is equivalent to a fixed size array allocation. Avoiding dynamic allocation, when possible, leads to small performance improvements. - Char indexing was converted to numeric indexing using a simple map (the one you’ve seen above). This operation somehow reduces the execution time by 2-8%. I didn’t really have time to understand why.
- String concatenation was replaced with direct indexing. I removed the “
.” operator wherever it could have been swapped with an indexed access. This requires a previously initialized string. If you take a look at the code below, you’ll see the line$finalCode = str_repeat('-', $this->length). Minimizing string concatenations helps reducing memory usage and execution time.Finally, to address the memory problem caused by full indexing, I adopted a hybrid solution. Each node of the tree built by the algorithm is still a single char of the generated code. However, when the algorithm reaches a node with no matching leaves, the remaining chars are placed as a string in the leaf node. This way, no memory is wasted allocating a full branch of n nodes (where n is the number of chars in the code).
This picture shows you the resulting array.

And here’s the code to do that:
/**
* @param integer $amount
* @return array
*/
function generate($amount)
{
$codes = [];
$number = 0;
$string = "";
$finalCode = str_repeat('-', $this->length);
$completeCodes = new SplFixedArray($amount);
$index = 0;
do
{
$number = bin2hex(openssl_random_pseudo_bytes($this->length));
if($this->useLetters)
{
$string = base_convert($number, 16, 20);
$string = strtr($string, $this->fromChars, $this->toChars);
}
else
{
$string = base_convert($number, 16, 10);
}
$string = substr($string, 0, $this->length);
$chars = str_split($string);
if(!$this->isInArray($chars, $codes, 0))
{
$finalCode = str_repeat('-', $this->length);
$this->addToarray($chars, $codes, 0, $finalCode);
$completeCodes[$index] = $finalCode;
$index++;
}
} while($index < $amount);
unset($codes);
return $completeCodes;
}
/**
* @param array $chars
* @param array $codes
* @param integer $index
* @return bool
*/
private function isInArray(&$chars, &$codes, $index)
{
if($index < $this->length - 2 && !is_array($codes))
{
if($codes == implode("", array_slice($chars, $index+1))) return true;
return false;
}
if(!isset($codes[$this->map[$chars[$index]]])) return false;
else
{
if($index == $this->length - 2)
return $codes[$this->map[$chars[$index]]] == $chars[$index+1];
if($index < $this->length - 2)
{
return $this->isInArray($chars, $codes[$this->map[$chars[$index]]], ++$index);
}
}
return false;
}
/**
* @param array $chars
* @param array $codes
* @param integer $index
* @param string $finalCode
*/
private function addToarray(&$chars, &$codes, $index, &$finalCode)
{
if($index < $this->length - 2)
{
if(!is_array($codes))
{
$code = $codes;
$codes = [];
$codes[$this->map[$code[0]]] = substr($code, 1);
$finalCode = substr($finalCode, 0, $index).implode("", array_slice($chars, $index));
return;
}
if(count($codes) == 1 && isset($codes[0]) && !is_array($codes[0]))
{
$code = $codes[0];
unset($codes[0]);
$codes[$this->map[$code[0]]] = substr($code, 1);
}
if(!isset($codes[$this->map[$chars[$index]]]))
{
$codes[$this->map[$chars[$index]]][] = implode("", array_slice($chars, $index+1));
$finalCode = substr($finalCode, 0, $index).implode("", array_slice($chars, $index));
return;
}
$finalCode[$index] = $chars[$index];
$this->addToarray($chars, $codes[$this->map[$chars[$index]]], ++$index, $finalCode);
}
else{
$codes[$this->map[$chars[$index]]][] = $chars[$index+1];
$finalCode[$index] = $chars[$index];
$finalCode[$index+1] = $chars[$index+1];
}
}To test the efficiency of this algorithm, I used it in a simple script to generate a number of alphanumeric codes 13 chars long. Time and memory scaling was measured generating a progressively larger pool of codes, starting from 100 and up to 100000.
Here’s the snippet I used:
$codeLength = 13;
$config = array(
[$codeLength, 100],
[$codeLength, 1000],
[$codeLength, 10000],
[$codeLength, 20000],
[$codeLength, 50000],
[$codeLength, 100000]
);
$r = new RandomCodeGenerator();
$r->useLetters(true);
foreach ($config as $k => $c)
{
$r->setLength($c[0]);
$start = microtime(true);
$codes = $r->generate($c[1]);
$time_elapsed_secs = microtime(true) - $start;
echo ($k+1).") ". $c[1]." codes of ".$c[0]." chars generated in ".$time_elapsed_secs." seconds, using ".(convert(memory_get_peak_usage()))."(".convert(memory_get_peak_usage(true)).") Mb of memory\n";
unset($codes);
}
function convert($size)
{
$unit=array('b','kb','mb','gb','tb','pb');
return @round($size/pow(1024,($i=(int)floor(log($size,1024)))),2).' '.$unit[$i];
}Running the script five times generated the following output:
1) 100 codes of 13 chars generated in 0.0065100193023682 seconds, using 197.44 kb(256 kb) Mb of memory 2) 1000 codes of 13 chars generated in 0.070569038391113 seconds, using 541.69 kb(768 kb) Mb of memory 3) 10000 codes of 13 chars generated in 0.72008204460144 seconds, using 3.85 mb(4 mb) Mb of memory 4) 20000 codes of 13 chars generated in 1.5691809654236 seconds, using 7.58 mb(7.75 mb) Mb of memory 5) 50000 codes of 13 chars generated in 5.1392588615417 seconds, using 18.59 mb(18.75 mb) Mb of memory 6) 100000 codes of 13 chars generated in 15.974501848221 seconds, using 37.03 mb(37.25 mb) Mb of memory 1) 100 codes of 13 chars generated in 0.010644912719727 seconds, using 199.01 kb(256 kb) Mb of memory 2) 1000 codes of 13 chars generated in 0.091349124908447 seconds, using 524.4 kb(768 kb) Mb of memory 3) 10000 codes of 13 chars generated in 1.0962328910828 seconds, using 3.7 mb(3.75 mb) Mb of memory 4) 20000 codes of 13 chars generated in 2.3688068389893 seconds, using 7.24 mb(7.25 mb) Mb of memory 5) 50000 codes of 13 chars generated in 6.7309219837189 seconds, using 17.94 mb(18 mb) Mb of memory 6) 100000 codes of 13 chars generated in 19.038684129715 seconds, using 35.77 mb(36 mb) Mb of memory 1) 100 codes of 13 chars generated in 0.0079169273376465 seconds, using 198.93 kb(256 kb) Mb of memory 2) 1000 codes of 13 chars generated in 0.079500913619995 seconds, using 524.67 kb(768 kb) Mb of memory 3) 10000 codes of 13 chars generated in 0.97308397293091 seconds, using 3.71 mb(3.75 mb) Mb of memory 4) 20000 codes of 13 chars generated in 2.2112140655518 seconds, using 7.25 mb(7.5 mb) Mb of memory 5) 50000 codes of 13 chars generated in 6.6483879089355 seconds, using 17.94 mb(18 mb) Mb of memory 6) 100000 codes of 13 chars generated in 19.41635799408 seconds, using 35.79 mb(36 mb) Mb of memory 1) 100 codes of 13 chars generated in 0.013813018798828 seconds, using 198 kb(256 kb) Mb of memory 2) 1000 codes of 13 chars generated in 0.1158139705658 seconds, using 525.2 kb(768 kb) Mb of memory 3) 10000 codes of 13 chars generated in 1.4209940433502 seconds, using 3.7 mb(3.75 mb) Mb of memory 4) 20000 codes of 13 chars generated in 3.1798701286316 seconds, using 7.24 mb(7.5 mb) Mb of memory 5) 50000 codes of 13 chars generated in 9.695641040802 seconds, using 17.97 mb(18 mb) Mb of memory 6) 100000 codes of 13 chars generated in 20.061115026474 seconds, using 35.8 mb(36 mb) Mb of memory 1) 100 codes of 13 chars generated in 0.0072038173675537 seconds, using 198.16 kb(256 kb) Mb of memory 2) 1000 codes of 13 chars generated in 0.076184988021851 seconds, using 523.16 kb(768 kb) Mb of memory 3) 10000 codes of 13 chars generated in 0.89858508110046 seconds, using 3.7 mb(3.75 mb) Mb of memory 4) 20000 codes of 13 chars generated in 1.9903841018677 seconds, using 7.25 mb(7.5 mb) Mb of memory 5) 50000 codes of 13 chars generated in 5.9241991043091 seconds, using 17.95 mb(18 mb) Mb of memory 6) 100000 codes of 13 chars generated in 17.208770990372 seconds, using 35.81 mb(36 mb) Mb of memory
Results obtained on this machine:
– Intel core i7 2600 @ 3.40 GHz
– RAM 16GB DDR3 800MHz
– PHP 5.5.12
– Windows 8.1
Although it is not exactly linear, the relation between the number of generated codes and time and memory usage is acceptable. To visualize the differences among the algorithms in terms of performance, in the following image you’ll find some nice plots.
The first row represents data from the original algorithm.
The second row represents the fully indexed solurion.
The last row represents the hybrid solution.

Got any comments or suggestions? Leave me a note below!